If the Last Row Has a Negative Constant Do You Pivot Again for Shortcut Method

Gaussian elimination is probably the best method for solving systems of equations if you lot don't have a graphing calculator or calculator programme to help you.

The goals of Gaussian elimination are to make the upper-left corner element a one, utilise uncomplicated row operations to go 0s in all positions underneath that first 1, get 1s for leading coefficients in every row diagonally from the upper-left to the lower-correct corner, and become 0s beneath all leading coefficients. Basically, you eliminate all variables in the concluding row except for one, all variables except for two in the equation to a higher place that one, and then on then along to the tiptop equation, which has all the variables. Then y'all can utilise dorsum substitution to solve for one variable at a time past plugging the values you know into the equations from the bottom up.

You accomplish this elimination by eliminating the x (or whatever variable comes showtime) in all equations except for the beginning ane. Then eliminate the second variable in all equations except for the get-go two. This process continues, eliminating one more than variable per line, until only one variable is left in the last line. And then solve for that variable.

Y'all can perform three operations on matrices in social club to eliminate variables in a system of linear equations:

• Yous can multiply whatever row by a constant (other than nil).

  

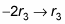
  multiplies row three by –2 to requite you a new row three.

• You lot tin switch any two rows.

  

  swaps rows i and two.

• You can add 2 rows together.

  

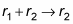
  adds rows one and 2 and writes information technology in row ii.

You can even perform more than one operation. You lot can multiply a row by a constant and and then add together it to another row to modify that row. For example, you can multiply row one past 3 and and then add that to row two to create a new row ii:

Consider the following augmented matrix:

At present take a look at the goals of Gaussian elimination in order to consummate the following steps to solve this matrix:

1. Complete the starting time goal: to get i in the upper-left corner.

   You already have it!

2. Consummate the second goal: to get 0s underneath the 1 in the first column.

   Yous need to utilise the combo of two matrix operations together here. Here'due south what you should ask: "What practice I need to add to row ii to make a ii become a 0?" The answer is –two.

   This step can be achieved by multiplying the start row by –2 and calculation the resulting row to the 2nd row. In other words, y'all perform the functioning

   

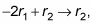
   which produces this new row:

   1. (–2 –4 –6 : 14) + (2 –iii –5 : 9) = (0 –seven –11: 23)

   You lot at present have this matrix:

   

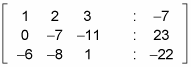
3. In the third row, go a 0 nether the one.

   To practise this step, you demand the operation

   

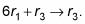
   With this adding, you should now have the following matrix:

   

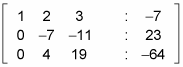
4. Become a ane in the second row, 2nd column.

   To exercise this step, yous demand to multiply by a constant; in other words, multiply row two past the appropriate reciprocal:

   

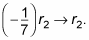
   This calculation produces a new second row:

   

5. Become a 0 under the i you created in row two.

   Back to the good onetime combo operation for the third row:

   

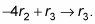
   Here's yet another version of the matrix:

   

6. Go another ane, this time in the tertiary row, third column.

   Multiply the third row past the reciprocal of the coefficient to become a one:

   

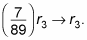
   You've completed the master diagonal after doing the math:

   

Y'all now have a matrix in row echelon form, which gives you lot the solutions when y'all apply back commutation (the terminal row implies that 0x + 0y + 1z = four, or z = –4). However, if you want to know how to get this matrix into reduced row echelon grade to notice the solutions, follow these steps:

1. Get a 0 in row 2, column three.

   Multiplying row three by the constant –eleven/seven and then adding rows two and three

   

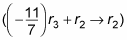
   gives you lot the post-obit matrix:

   

2. Get a 0 in row ane, column three.

   The operation

   

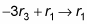
   gives you the following matrix:

   

3. Get a 0 in row one, column ii.

   Finally, the operation

   

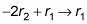
   gives you this matrix:

   

This matrix, in reduced row echelon form, is really the solution to the system: x = –one, y = 3, and z = –iv.

Well-nigh This Article

Well-nigh the book author:

Mary Jane Sterling nada algebra, business calculus, geometry, and finite mathematics at Bradley Academy in Peoria, Illinois for more than than xxx years. She is the author of several For Dummies books, including Algebra Workbook For Dummies, Algebra II For Dummies, and Algebra II Workbook For Dummies.

This commodity tin can exist constitute in the category:

• Pre-Calculus ,

danielspoxim2000.blogspot.com

Source: https://www.dummies.com/article/academics-the-arts/math/pre-calculus/how-to-use-gaussian-elimination-to-solve-systems-of-equations-167828

Share this post